Given a Binary Tree, write a function which calculates the difference between the sum of node values at odd levels and sum of node values at even levels.
Consider the root node is at height 1.
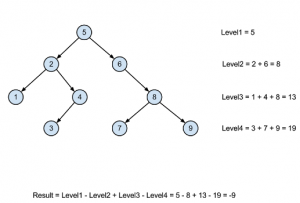
The solution is short and uses recursion. The idea is that you negate all levels under the current one (the level of the current node) and you do that on each step of the recursion.
sum[l1] – (sum[l2] – (sum[l3] – (sum[l4] – … = sum[l1] – sum[l2] + sum[l3] – sum[l4]…
int getDifference(Tree *root) {
if (root == null) {
return 0;
}
int result = root->data - geteDifference(root->left)
- getDifference(root->right);
return result;
}


can you please help with tracing this recursion?
Hi Aniket,
Here is the break down of the formula, where for example n1 is the node with value 1, and so on:
root->data – calc(root->left) – calc(root->right)=
5 – calc(n2) – calc(n6)=
5 – (2 – calc(n1) – calc(n4)) – (6 – 0 – calc(n8))=
//… skip a few rows
5 – (2 – (1 – 0 – 0) – (4 – 3)) – (6 – 0 – (8 – 7 – 9)) = -9
Hope this is clear..
A variety of terms have actually been made use oof to describe this:
crowd-sourcing, wisdom of crowds, peer production, wikinomics (Benkler, 2006; Howe, 2008; Surowiecki, 2004;
Tapscott andd Williams, 2006).
int diff_sum_nodes_odd_even(node *root, int multiplier) {
if (!root)
return 0;
else {
int sum = root->val*multiplier;
multiplier *= -1;
sum += diff_sum_nodes_odd_even(root->left,multiplier);
sum += diff_sum_nodes_odd_even(root->right,multiplier);
return sum;
}
}