Heap data structure is an array object that can be viewed as a nearly complete binary tree. Each node of the tree corresponds to an element of the array. The tree is completely filled on all levels except possibly the lowest , which is filled from the left up to a point.
There are two kinds of binary heaps: max-heaps and min-heaps. In a max-heap , the max-heap property is that for every node i other than the root, the value of a node is at most the value of its parent. Thus , the largest element in a max-heap is stored at the root. A min-heap is organized in the opposite way, each node is less than or equal to each of its children. Min-heaps are often used to implement priority queues.
Viewing a heap as a tree and a heap of n elements in based on a complete binary tree,its height is O(log n). Basic operations like insert,delete on heaps run in time at most proportional to the height of the tree and the take O(log n) time.
We’ll discuss about some important procedure of Heap.
For heaps we assume the following operations
A[i] – value at node (element) i
LEFT(i) – index of left child node = 2i
RIGHT(i) – index of right child node = 2i + 1
PARENT(i) – index of parent node = i / 2
Max-Heapify : Given a tree that is a heap except for node i,Max-Heapify function arranges node i and it’s subtrees to satisfy the heap property.
MAX-HEAPIFY(A,i)
l = LEFT(i)
r = RIGHT(i)
if l <= A.heapsize and A[l] > A[i]
largest = l
else
largest = i
if r <= A.heapsize and A[r] > A[largest]
largest = r
if largest != i
exchange A[i] with A[largest]
MAX-HEAPIFY(A,largest)
Time Complexity of Max-Heapify on a node of height h is O(h).
Build Max-Heap : Using MAX-HEAPIFY() we can construct a max-heap by starting with the last node that has children (which occurs at A.length/2 the elements the array A.(length/2+1) to A.n are all leaves of the tree ) and iterating back to the root calling MAX-HEAPIFY() for each node which ensures that the max-heap property will be maintained at each step for all evaluated nodes. The pseudocode for the routine is
BUILD-MAX-HEAP(A)
A.heapsize = A.length
for i = A.length/2 downto 1
MAX-HEAPIFY(A,i)
Time Complexity of Build-MAX-HEAP procedure is O(n).
Heapsort: Once we have created a max-heap, to sort the elements we simply swap the root with the last node in the heap (since the root is guaranteed to be the maximum remaining element) and remove it from the heap (note it will still be in the array but in sorted order at the back of the array) rebuild the max-heap by calling MAX-HEAPIFY on the root repeat the procedure until there are only two nodes remaining in the heap.
The pseudocode for heapsort is
HEAPSORT(A)
BUILD-MAX-HEAP(A)
for i = A.length downto 2
exchange A[1] with A[i]
A.heapsize = A.heapsize - 1
MAX-HEAPIFY(A,1)
Time Complexity of HEAPSORT Procedure is O(n log n).

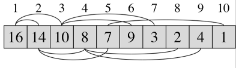


why the array starts with index why not with index 0 as in case of Arrays
Heap is a mathematical concept where indexing start as 1. When implementing the idea in programming paradigm then the formula can be adjusted as per the language of choice as many of them uses zero as starting point then the formula can be represented as-
left – 2i+1
right – 2i+2
parent – i/2-1