In Previous Post We learned about In-Order Successor.In this post ,We’ll learn what is In-Order Predecessor.
The predecessor of a node x in a search tree is the node with largest key that belongs to the tree and that is strictly less than x’s key.
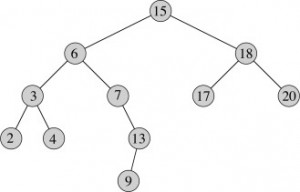
In above binary search tree, in-order predecessor of 17 is 15 , predecessor of 6 is 4 and predecessor of 13 is 9.
Method to find out In-Order Predecessor is quite similar to Successor.
Method 1:
int maxValue(struct node* node)
{
struct node* n = node;
while(n->right!=NULL)
n=n->right;
return n;
}
struct node* inOrderPredecessor(struct node* root,struct node* x)
{
if(x->left)
return maxValue(x->left);
else
{
struct node* y = x->parent;
while(y !=NULL && x == y->left)
{
x = y;
y = y->parent;
}
return y;
}
}
Time Complexity : O(h) where h is the height of tree.
Method 2:
struct node* inOrderPredecessor(struct node* root, struct node* x)
{
if( x->left != NULL )
return maxValue(x->left);
struct node *predecessor = NULL;
while (root != NULL)
{
if (x->data > root->data)
{
predecessor = root;
root = root->right;
}
else if (x->data < root->data)
root = root->left;
else
break;
}
return predecessor;
}
Time Complexity : O(h)


I guess there is a bug in the Method 1:
You have not declared the variable “y”. I guess it should of Node type, meaning:
Node y;
Thanks,
Aditya
return type of max value is int or struct node* type
Alternate solution proposal. Can we do something like the following.
Do traditional In order traversal and instead of printing, put the value in a queue or an array. The next step of finding predecessor or successor is an easy one.
What if the number of elements are 1 millions? Are you going to follow this traditional in order traversal, complexity you know is then O(n). For less comlexity we use the upper method.