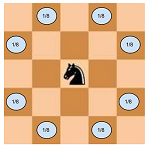
Given the size of the chess board and initial position of the knight, what is the probability that after k moves the knight will be inside the chess board.
Note:-
1) The knight makes its all 8 possible moves with equal probability.
2) Once the knight is outside the chess board it cannot come back inside.
Algorithm:
Start with the initial coordinates of the knight. Make all possible moves for this position and multiply these moves with their probability, for each move recursively call the function continue this process till the terminating condition is met. Terminating condition is if the knight is outside the chess board, in this case return 0, or the desired number of moves is exhausted, in this case return 1.
As we can see that the current state of the recursion is dependent only on the current coordinates and number of steps done so far. Therefore we can memoize this information in a tabular form.
Solution:
#define MAXSIZE 100
#define MAXK 100
double dp[MAXSIZE][MAXSIZE][MAXK];
int vis[MAXSIZE][MAXSIZE][MAXK]; //stores 1 if there is a corresponding dp entry, 0 otherwise
double prob_knight(int x, int y, int size, int step, int k)
{
//if knight is outside the board
if(x < 0 || y < 0 || x >= size || y >= size) return 0;
//if all moves are exhausted
if(step == k) return 1;
//if dp table has the this value stored return it
if(vis[x][y][k] != 0)
return dp[x][y][k];
vis[x][y][step] = 1;
//all possible x direction's for knight to move
int dirx[] = {2, 2, -2, -2, 1, 1, -1, -1};
//corresponding y direction for knight
int diry[] = {1, -1, 1, -1, 2, -2, 2, -2};
double ans = 0;
for(int i = 0;i < 8; ++i){
//knight makes the next move with probability (1 / 8)
ans = ans + ((double)1 / (double)8) * prob_knight(x + dirx[i], y + diry[i], size, step + 1, k);
}
//update the dp table
dp[x][y][k] = ans;
return ans;
}
Expected time complexity:
O((n ^ 2) * k) where n is the size of the board and k is the number of moves.
Expected space complexity:
O((n ^ 2) * k) where n is the size of the board and k is the number of moves.