Euler Function: In number theory, Euler’s totient function (or Euler’s phi function), denoted as φ(n) or ϕ(n), is an arithmetic function that counts the positive integers less than or equal to n that are relatively prime to n , i.e., the numbers whose GCD (Greatest Common Divisor) with n is 1. (These integers are sometimes … Read More →
Euclid’s Algorithm (Greatest Common Divisor) – GCD
Given two non-negative integers a and b. We need to find their greatest common divisor (GCD), ie, the largest number that divides both a and b. When it is of the numbers is zero, and the other is non-zero, their greatest common divisor, by definition, it is the second number. When both numbers are zero, … Read More →
House Robber | Dynamic Programming
Problem: You have n houses with certain amount of money stashed in each house. You can not steal any adjacent houses. Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can steal. Solution: This is a simple dynamic programming problem. The key is … Read More →
Design of a Tinyurl Service
What is tinyurl? A tinyurl service compresses a long url into a short one. This saves space, and is useful for scenarios such as twitter or weibo, where each character counts. The down side is possible spam use. Concerns include longevity of a short url. i.e. “http://tiny.me/5ie0V2″. The highlight part can be any string with … Read More →
Word Ladder Problem
Problem: Given two words (start and end), and a dictionary, find the length of shortest transformation sequence from start to end, such that: Only one letter can be changed at a time. Each intermediate word must exist in the dictionary For example, Given: start = “hit” end = “cog” dict = ["hot","dot","dog","lot","log"] As one shortest … Read More →
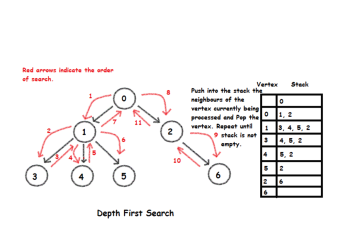
Depth-first search (DFS) – Algorithms and Data Structures
Depth-first search starts a graph’s traversal by visiting an arbitrary vertex and marking it as visited. On each iteration, the algorithm proceeds to an unvisited vertex that is adjacent to the one it is currently in. (If there are several such vertices, a tie can be resolved arbitrarily. As a practical matter, which of the … Read More →
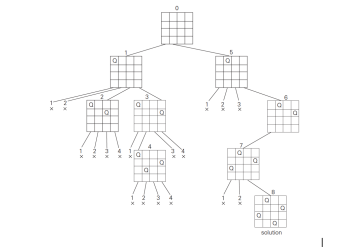
N Queens – Backtracking Problem 2
BackTracking: Find a solution by trying one of several choices. If the choice proves incorrect, computation backtracks or restarts at the point of choice and tries another choice. It is often convenient to maintain choice points. In an exhaustive search algorithm you search every possible choice to reach to the goal state, however, the backtracking … Read More →
Set every cell in matrix to 0 if that row or column contains a 0
Given a m x n matrix, if an element is 0, set its entire row and column to 0. Do it in place. This problem should be solved in place, i.e., no other array should be used. We can use the first column and the first row to track if a row/column should be set … Read More →
Distinct Subsequences
Given a string S and a string T, count the number of distinct subsequences of T in S. A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, “ACE” is … Read More →
Min Stack Problem
Design a stack that supports push, pop, top, and retrieving the minimum element in constant time. push(x) — Push element x onto stack. pop() — Removes the element on top of the stack. top() — Get the top element. getMin() — Retrieve the minimum element in the stack. Solution: the StackMin class which keeps the … Read More →
Finding All the Subsets of a Set – Backtracking Problem
Given a set of distinct integers, S, return all possible subsets. Note: Elements in a subset must be in non-descending order. The solution set must not contain duplicate subsets. For example, If S = [1,2,3], a solution is: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ] We use the backtracking method to solve … Read More →


What’s going on ?