Depth-first search starts a graph’s traversal by visiting an arbitrary vertex and marking it as visited. On each iteration, the algorithm proceeds to an unvisited vertex that is adjacent to the one it is currently in. (If there are several such vertices, a tie can be resolved arbitrarily. As a practical matter, which of the … Read More →
Union and Intersection of two Linked Lists
Given two Linked Lists, create union and intersection lists that contain union and intersection of the elements present in the given lists. Order of elments in output lists doesn’t matter. Following are simple algorithms to get union and intersection lists respectively. Intersection (list1, list2) Initialize result list as NULL. Traverse list1 and look for its … Read More →
Graph Data Structure
Graphs A tree only allows a node to have children, and there cannot be any loops in the tree, with a more general graph we can represent many different situations. A very common example used is flight paths between cities. If there is a flight between city A and city B there is an edge … Read More →
Min Stack Problem
Design a stack that supports push, pop, top, and retrieving the minimum element in constant time. push(x) — Push element x onto stack. pop() — Removes the element on top of the stack. top() — Get the top element. getMin() — Retrieve the minimum element in the stack. Solution: the StackMin class which keeps the … Read More →
Sort an almost sorted array where only two elements are swapped
Problem: Given an almost sorted array where only two elements are swapped, how to sort the array efficiently? Expected time complexity is O(n) and only one swap operation to fix the array. Input: arr[] = {1, 5, 3} // 3 and 5 are swapped Output: arr[] = {1, 3, 5} The idea is to traverse … Read More →
Trie Data Structure – C Implementation
Trie Tree: A trie (from retrieval), is a multi-way tree structure useful for storing strings over an alphabet. It has been used to store large dictionaries of English (say) words in spelling-checking programs and in natural-language “understanding” programs. A trie tree uses the property that if two strings have a common prefix of length n … Read More →
Implement Stack and Queue using Linked List in Java
The implementation of a linked list is pretty simple in Java. Each node has a value and a link to next node. Two popular applications of linked list are stack and queue. Stack: What is stack? Stack is a linear data structure which implements data on last in first out criteria. Here is a java … Read More →
Repeatedly Delete N nodes after M nodes of a Linked list
Given a linked list and two integers M and N. Traverse the linked list such that you retain M nodes then delete next N nodes, continue the same until end of the linked list. Input: M = 2, N = 2 Linked List: 1->2->3->4->5->6->7->8 Output: Linked List: 1->2->5->6 The main part of the problem is … Read More →
Count Pairs of Numbers with a Given Difference K
Given an unsorted array and a number n, find if there exists a pair of elements in the array whose difference is n. Return count of such pairs. Example k=4 and a[]={7,623,19,10,11,9,3,15} Output should be : 6 Pairs can be: 7,11 7,3 6,10 19,23 15,19 15,11 Solution: Time Complexity: O(NLogN) Space Complexity: O(1)
Merging 2 Arrays without using Extra Space
Given two sorted arrays, A and B. Write a method merging the elements of B into A in sorted order. Assume A has a large enough buffer at the end to hold all of B’s elements. Solution: Suppose we want to merge two arrays a1 and a2. a1 has n elements and has space for … Read More →
Minimum Distance Between Array Elements
Given a non-negative integer array, Find the minimum distance between 2 distinct elements of A. Minimum Distance is defined as if P != Q then |(A[P] – A[Q])| Solution: Time Complexity: O(N)

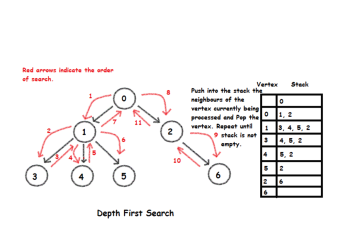
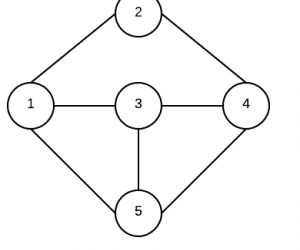

What’s going on ?