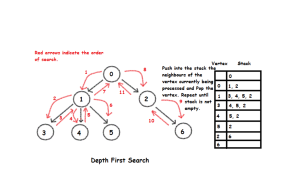
Depth-first search starts a graph’s traversal by visiting an arbitrary vertex and marking it
as visited. On each iteration, the algorithm proceeds to an unvisited vertex that
is adjacent to the one it is currently in. (If there are several such vertices, a tie
can be resolved arbitrarily. As a practical matter, which of the adjacent unvisited
candidates is chosen is dictated by the data structure representing the graph. In
our examples, we always break ties by the alphabetical order of the vertices.) This
process continues until a dead end—a vertex with no adjacent unvisited vertices—
is encountered.
At a dead end, the algorithm backs up one edge to the vertex
it came from and tries to continue visiting unvisited vertices from there. The
algorithm eventually halts after backing up to the starting vertex, with the latter
being a dead end. By then, all the vertices in the same connected component as the
starting vertex have been visited. If unvisited vertices still remain, the depth-first
search must be restarted at any one of them.
ALGORITHM DFS(G)
//Implements a depth-first search traversal of a given graph
//Input: Graph G = V, E
//Output: Graph G with its vertices marked with consecutive integers
// in the order they are first encountered by the DFS traversal
mark each vertex in V with 0 as a mark of being “unvisited”
count ←0
for each vertex v in V do
if v is marked with 0
dfs(v)
Implementation:
public class DepthFirstSearch {
private boolean[] marked;
private int count;
public DepthFirstSearch(Graph G, int s){
marked = new boolean[G.V()];
dfs(G,s);
}
private void dfs(Graph G, int v){
marked[v] = true;
count++;
for(int i:G.adj(v)){
if(!marked[i]){
dfs(G,i);
}
}
}
public boolean marked(int v) {
return marked[v];
}
public int count() {
return count;
}
}
Applications of DFS:
Following are the problems that use DFS as a building block.
1) For an unweighted graph, DFS traversal of the graph produces the minimum spanning tree and all pair shortest path tree. DFS is at the heart of Prims and Kruskals algorithms.
2) Detecting cycle in a graph
A graph has cycle if and only if we see a back edge during DFS. So we can run DFS for the graph and check for back edges.
3) Path Finding
DFS algorithm can be used to find a path between two given vertices u and z.
i) Call DFS(G, u) with u as the start vertex.
ii) Use a stack S to keep track of the path between the start vertex and the current vertex.
iii) As soon as destination vertex z is encountered, return the path as the
contents of the stack
4) Topological Sorting
DFS is an intermediate step for topological sorting.
5) Finding Strongly Connected Components of a graph A directed graph is called strongly connected if there is a path from each vertex in the graph to every other vertex. (See this for DFS based algo for finding Strongly Connected Components)
6) DFS is very helpful in solving almost all the maze puzzles. Most of the maze puzzles can be converted into Graph problems and traversals result into the solution. DFS can be adapted to find all solutions to a maze by only including nodes on the current path in the visited set.