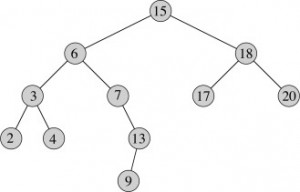
Given a node in binary search tree say x,the in-order successor of node x is the node with the smallest value greater than node x’s value.
In above binary search tree, in-order successor of 18 is 20, successor of 6 is 7 and successor of 13 is 15.
Algorithm : In in-order traversal of binary search tree we get number in ascending order.Hence the successor of a node will be either to the right of node(if exists) or one level above.
Method 1: (If Parent pointer is given)
The code for finding in-order successor is broken into two cases:
i) If the right subtree of node x is not empty then the successor of x is just the leftmost node in the right subtree.
ii) If the right subtree of node x is empty and x has a successor y,then y is the lowest ancestor of x whose left child is also an ancestor of x.
struct node* minValue(struct node* node)
{
struct node* n = node;
while(n->left!=NULL)
n=n->left;
return n;
}
struct node* inOrderSuccessor(struct node* root,struct node* x)
{
if(x->right)
return minValue(x->right);
else
{
y = x->parent;
while(y !=NULL && x == y->right)
{
x = y;
y = y->parent;
}
return y;
}
}
Time Complexity : O(h) where h is height of the tree,since we either follow a path up the tree or follow a path down the tree.
Method 2: (Without Parent pointer)
Steps:
i) If the right subtree of node x is not empty then the successor of x is just the leftmost node in the right subtree.(Same as step1 of above Method).
ii) If the right subtree of node x is empty then start from the root and keep doing following
a. if the root value is greater than node value then go to left subtree.
b. if the root value is less than node value then go to right subtree.
c. Stop when we reach the node.
struct node* inOrderSuccessor(struct node* root, struct node* x)
{
if( x->right != NULL )
return minValue(x->right);
struct node *successor = NULL;
while (root != NULL)
{
if (x->data < root->data)
{
successor = root;
root = root->left;
}
else if (x->data > root->data)
root = root->right;
else
break;
}
return successor;
}
Time Complexity : O(h) where h is height of the tree.


If node n is not present in the tree it should return null but it does not…should we add a check for such condition or are we assuming already that n is a part of the tree..??
Hi,
The Method 2 is incorrect.
I considered the following tree:
4
2 6
1 3 5 7
When I pass the node for 2, I get the 4 as the successor node (should be 3).
Similarly, when I pass in 6, I get Null as the successor node (should be 7).
Thanks!
It’s correct;
If you pass the node for 2, since node 2 has the right subtree , it falls in the first case
if( x->right != NULL )
return minValue(x->right);
And the minValue of the right subtree of 2 is 3. Therefore, it will return 3.
Same thing for the node 6.